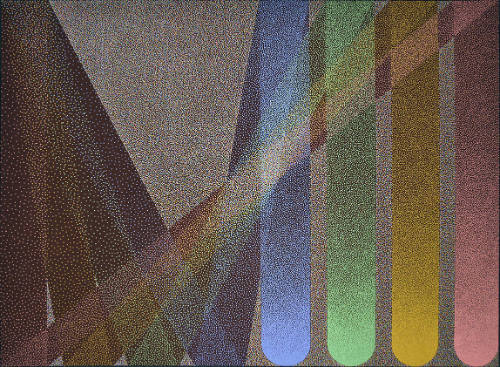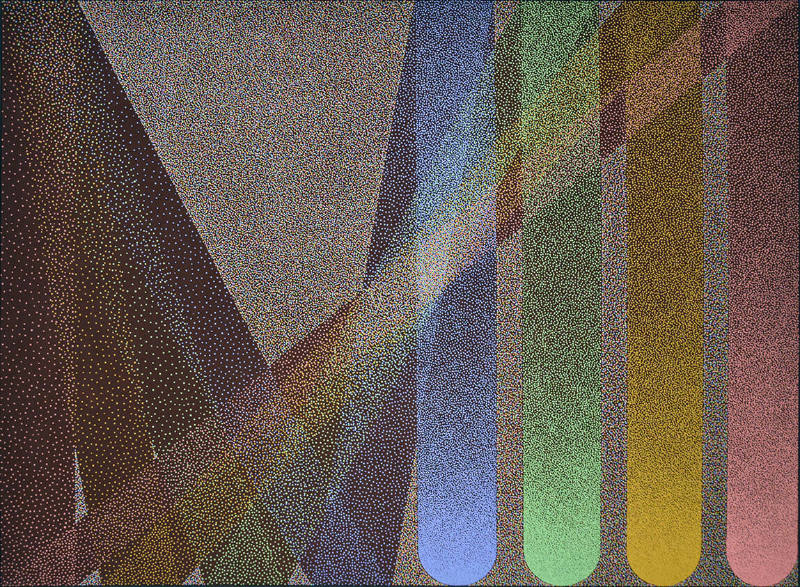Untitled
Date1976
Mediumacrylic on canvas
Dimensions70 3/4 × 93 1/2 × 1 1/2 inches (179.7 × 237.5 × 3.8 cm)
Portfolio/Series"Searchlights" series
Credit LineGift of Alfred and Lillian Hertel.
Object number2000.9.2
Copyright© Murray Reich.
The images and text contained on this page are owned by Telfair Museums or used by the Museum with permission from the owners. Unauthorized reproduction, transmission or display of these materials is prohibited with the exception of items deemed “fair use” as defined by U.S. and international copyright laws.Label TextMurray Reich was an American artist born in New York City in 1932. He was also a Professor Emeritus of Painting at Bard College in New York, where he taught for more than 25 years. For Reich, painting and artmaking was an intellectual pursuit. He likened his artistic practice to that of exploring and investigating, and as a painter he was constantly questioning. Reich enjoyed establishing systems of order and inquiry that allowed him a structure with which to respond visually, while at the same time finding joy in circumventing the laws he had established. Reich wants viewers of his work to be taken in by illusion, while also understanding the framework that created the illusion in the first place.
It was a common practice for Reich to leave his paintings untitled unless a specific name presented itself to him. This 1976 work is part of Reich’s 'Searchlights' series, where he was interested in optical color mixing and illusionistic space versus mere surface, and how each individual’s perception affects this balance. The painting comprises the four primary colors plus the ground color, with the value of each color adjusted to create the illusion of depth and movement alluding to a beam of light. The whole composition is created using dots that fluctuate their distance between each other, similar to the Pointillism technique created by Georges Seurat at the end of the 19th century. Additionally, Reich was interested in a spatial dimension drawn from his expertise in sports, and the way an angle can be created and how it leads to an intentional outcome.